Research
Brain Dynamics Toolbox
The Brain Dynamics Toolbox is open matlab software for exploring user-defined dynamical systems with minimal programming effort. It solves initial-value problems in systems of ODEs, DDEs, SDEs and PDEs. Users define their system of equations as a custom matlab function. Interchangeable solvers and graphical plotting tools can then be applied to it with no additional programming effort. The toolbox is available from bdtoolbox.org.

Heitmann S, Breakspear M (2023) Handbook for the Brain Dynamics Toolbox: Version 2023. bdtoolbox.org. ISBN 978-0-6450669-3-7.
Heitmann S, Aburn M, Breakspear M (2017) The Brain Dynamics Toolbox for Matlab. Neurocomputing Vol 315. p82-88. doi:10.1016/j.neucom.2018.06.026
Assessing drugs for cardiotoxicity
Many classes of drugs cause potentially fatal arrhythmias by interfering with the electrical properties of heart cells. International safety guidelines thus require all new drugs to be tested in living cells prior to human trials. Computer models offer an ethical alternative but are difficult to deploy outside of specialist computing laboratories. We solved the problem by using computer simulation to identify the principal axis of arrhythmia in cardiac electrophysiology. The axis serves as a yardstick for pharmacologists to assess the arrhythmogenic risk of any drug without animals nor bespoke computer simulations.
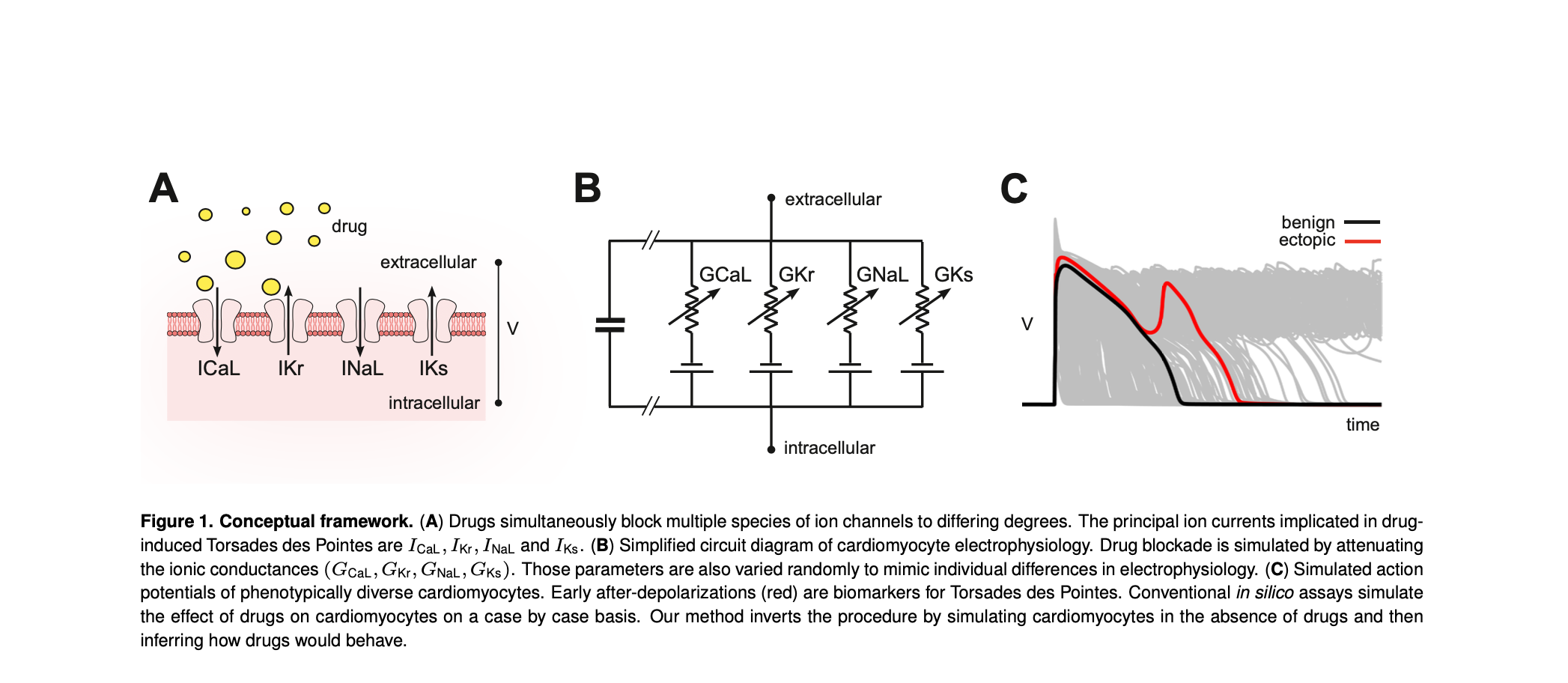
Heitmann S, Vandenberg J, Hill A (2023) Assessing drug safety by identifying the axis of arrhythmia in cardiomyocyte electrophysiology. eLife.
doi:10.7554/eLife.90027.
Arrhythmogenesis as the failure of repolarization
Atrial fibrillation typically arises from the anatomical site where the pulmonary veins attach to the heart wall. Nobody knows why. We used dynamical systems theory to show that arrhythmias can be triggered by cardiac cells that fail to repolarize of their own accord. Technically, these cells are said to be bistable because they can dwell in either the resting state or the depolarized state.
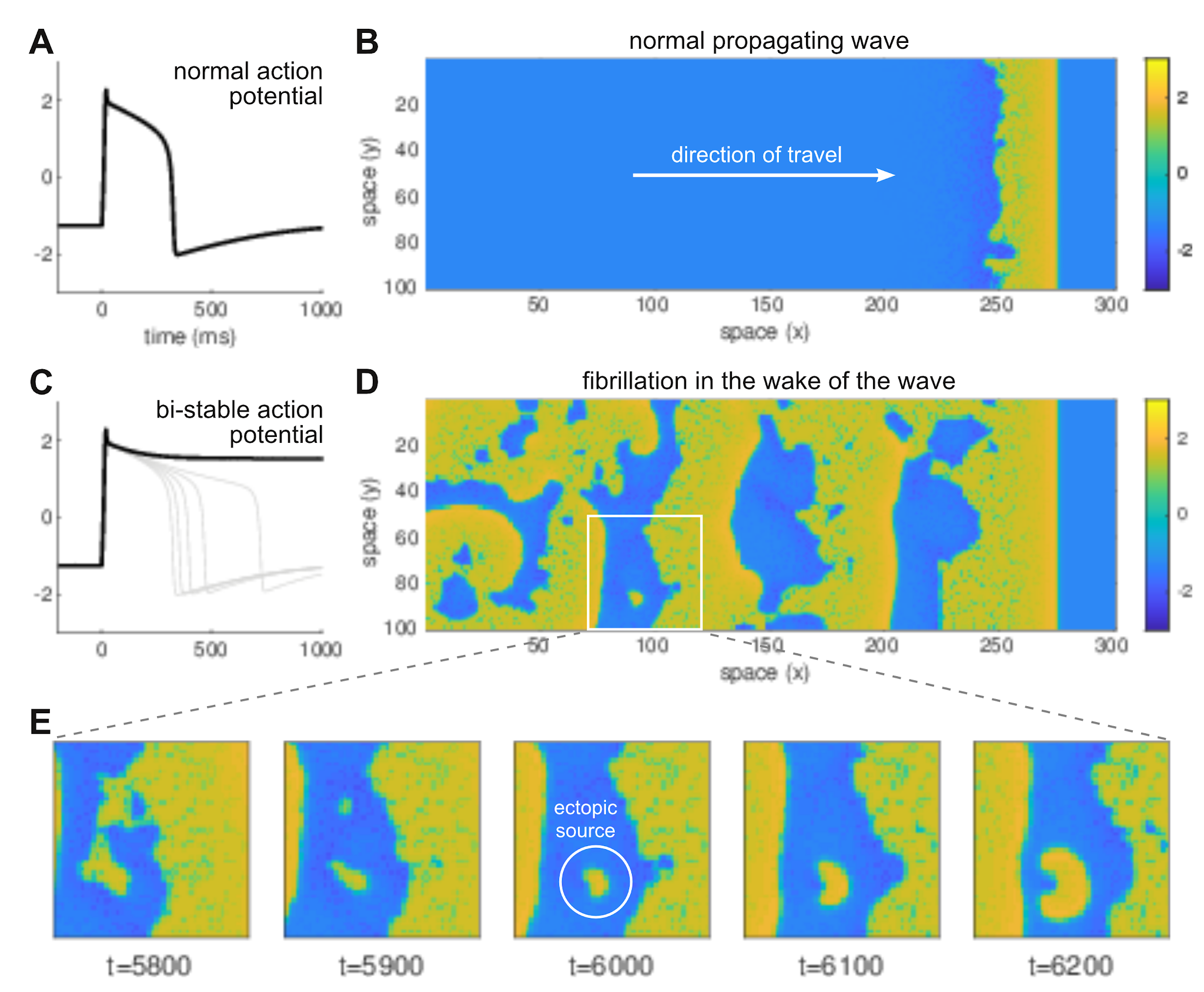
Our analysis showed that the heart can support normal travelling waves despite the presence of large numbers of bistable cells. However there is a limit and tissue boundaries are especially susceptible to arrhthymia. This may explain why atrial fibrillation often emanates from the cuff of the pulmonary vein.
Heitmann S, Shpak A, Vandenberg J, Hill A (2021) Arrhythmogenic effects of ultra-long and bistable cardiac action potentials. PLoS Computational Biology 17(2): e1008683.
Direction-selective visual motion detection
Neurons of the visual cortex are known to respond selectively to the direction of visual motion. Mathematically, the response characteristics of the neurons cannot be constructed from separate spatial and temporal processes. It is unknown how these neurons work without resort to explicit time delays in the circuitry.
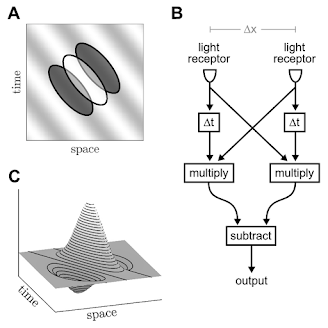
We proposed a novel neural mechanism that relies on travelling waves in the cortical tissue insetad of time delays. We showed that endogenously generated waves can resonate with the space-time signature of the visual stimulus to selectively respond to visual motion. The speed and direction of the waves are governed entirely by the profile of the lateral-inhibitory coupling.
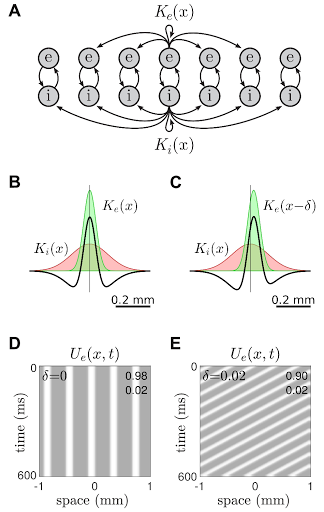
Heitmann & Ermentrout (2020) Direction-Selective Motion Discrimination by Traveling Waves in Visual Cortex. PLoS Computational Biology 16(9): e1008164.
Heitmann & Ermentrout (2016) Propagating Waves as a Cortical Mechanism of Direction-Selectivity in V1 Motion Cells. Proc 9th EAI Intl Conf on Bio-inspired Info & Comm Tech. BICT’15. New York.
The mathematics of brain stimulation
Optogenetic techniques allow neurophysiologists to directly stimulate neurons with light. It is often assumed that the dynamical behaviour of the neural tissue is unchanged. However recent observations provide a clue that this may not be the case. Lu et al (2015) found that stimulation of macaque cortex elicited 40-80 Hz oscillations that were consistent with Type II neural excitability. Yet these oscillations propagated far into the surrounding cortical tissue. Whereas mathematical theory suggests that propagating waves are only supported by neural tissue with Type I excitability. So how can cortical tissue simultaneously exhibit both Type I and Type II excitability? We investigated the apparent contradiction by modelling the cortex as recurrently-connected excitatory and inhibitory neurons. We found that optogenetic stimulation can locally transform Type I excitability into Type II excitability by preferentially targeting inhibitory cells. The findings shed new light on how optogenetic stimulation can alter the response dynamics of neural tissue.
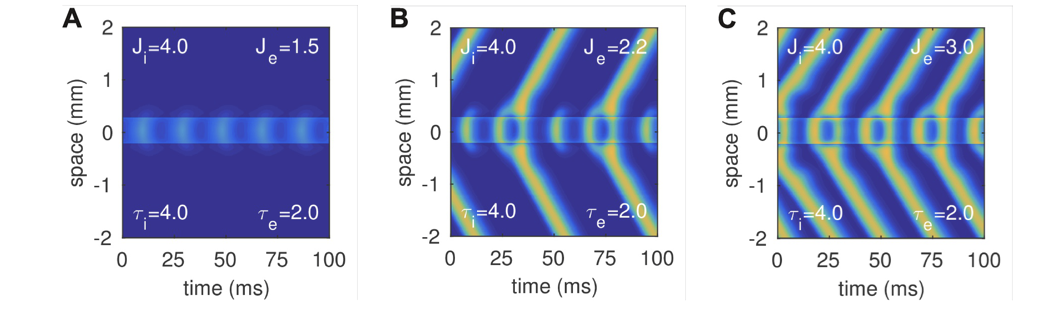 |
| Space-time plots of the cortical model in one spatial dimension. Optogenetic stimulation was applied focally at position x=0. Panels A-C show cases of weak, medium, and strong stimulation respectively. The model exhibits co-existing Type I and Type II excitability in agreement with neurophysiological observations. |
Heitmann, Rule, Truccolo, Ermentrout (2017) Optogenetic stimulation shifts the excitability of cerebral cortex from Type I to Type II: Oscillation onset and wave propagation. PLOS Computational Biology. 13(1): e1005349. doi: 10.1371/journals.pcbi.1005349
Lu, Truccolo, Wagnerm Varas-Irwin, Ozden, Zimmermann, May, Agha, Wang, Nurmikko (2015) Optogenetically induced spatiotemporal gamma oscillations and neuronal spiking activity in primate motor cortex. J Neurophysiol 113: 3574-3587.
The cortical origin of visual hallucinations
Geometric patterns of spirals, honeycombs and checker-boards are common themes in visual hallucinations. They are thought to originate from the neural circuitry of the primary visual cortex – the region of the brain which processes visual shapes.
 |
| Geometric visual hallucinations. A-D: LSD flashbacks painted by Oster (1970). E-F: Hallucinations by THC intoxication (Siegel & Jarvik, 1975). G: Hallucinations by occular pressure (Tyler, 1978). H: Migraine aura (Richards, 1971). Adapted from Billock & Tsou (2012) |
Our collaborators at the University of New South Wales devised a method for objectively measuring the visual hallucinations seen in stroboscopic flicker. In particular, they measured the spatial wavelength and speed of illusory blobs that appear to race around a ring-shaped stimulus when it is flickered at 10-20 Hz. As part of this study, we constructed a mathematical model of the visual cortex that reproduces the perceptual behaviour.
Pearson J, Chiou R, Rogers S, Wicken M, Heitmann S, Ermentrout GB (2016) Sensory dynamics of visual hallucinations in the normal population. eLife Vol 5. e17072.
Pattern formation in neural oscillators
The prevalence of synchronized neural spiking in the brain suggests a role in normal brain function. Neural synchronization can be modelled with coupled oscillators where the phase of each oscillator represents the timing of the neural spike. These models generate planar waves and spirals which resemble those observed in neural tissue.
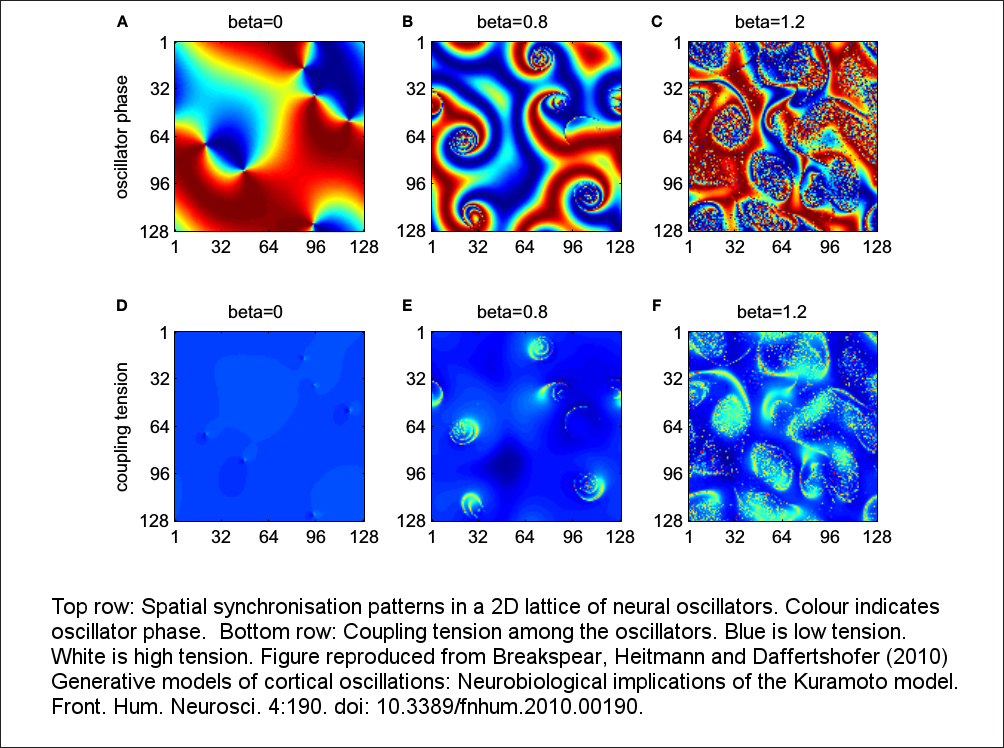
Breakspear M, Heitmann S, Daffertshofer A (2010). Generative models of cortical oscillations: Neurobiological implications of the Kuramoto model. Frontiers in Human Neuroscience 4:190.
Heitmann S, Ermentrout GB (2015) Synchrony, waves and ripple in spatially coupled Kuramoto oscillators with Mexican hat connectivity. Biological Cybernetics 109:3.
Motor commands as spatial oscillation patterns
Beta-band (15-30 Hz) neural oscillations are routinely observed in the human motor system but their purpose is unknown. We conjectured that the spatial arrangement of beta oscillations in cortex could serves as the neural substrate for encoding motor commands. We constructed a model of the descending motor system which shows how oscillatory patterns in cortex can be translated into specific muscle movements. The model demonstrates a functional role for beta oscillations that also replicates the known physiological changes of beta-band cortico-muscular coherence during movement.
Heitmann S, Boonstra T, Gong P, Breakspear M, Ermentrout GB (2015) The rhythms of steady posture: Motor commands as spatially organized oscillation patterns. Neurocomputing. Special Issue on Advances on Biological Rhythmic Pattern Generation 170.
Heitmann S, Boonstra T, Breakspear M (2013) A dendritic mechanism for decoding traveling waves: Principles and applications to motor cortex. PLOS Computational Biology.
Heitmann S, Gong P, Breakspear M (2012) A computational role for bistability and traveling waves in motor cortex. Frontiers in Computational Neuroscience 6:67.
Co-contraction of antagonist muscles
Co-contraction refers to the simultaneous contraction of antagonist muscles. It has no impact on joint torque but it does increase joint damping because of the non-linear force-velocity properties of muscle tissue. We analysed the stability of co-contracting muscle in a simulated biomechanical limb with realistic force-length-velocity relationships. We found that co-contraction not only modulates joint damping but that it also effects postural stability. Under certain conditions, co-contracting muscles can even induce multiple stable equilibrium points.
Heitmann S, Ferns N, Breakspear M (2012). Muscle co-contraction modulates damping and joint stability in a three-link biomechanical limb. Frontiers in Neurorobotics 5:5.